
바킹독님의 강의를 참고하였습니다.
https://blog.encrypted.gg/category/강좌/실전%20알고리즘
'강좌/실전 알고리즘' 카테고리의 글 목록
blog.encrypted.gg
+ 해당 카테고리엔 알고리즘 문제풀이와 관련된 내용을 업로드.
+ 기록해두고 싶은 부분만 정리해 둠.
알고리즘 설명

DFS : 다차원 배열에서 각 칸을 방문할 때 깊이를 우선으로 방문하는 알고리즘. (BFS는 너비)
예시

BFS 과정에서 다른 건 다 같고, 큐가 스택으로 바뀐 것뿐이다.
BFS때와 같이 예시를 보자.

(0,0)부터 이어진 파란색 칸을 확인할 것이다.
(0,0)을 밟은 상태에서 시작했으니, 해당칸에 표시를 남기고 스택에 넣는다. (초기세팅)
이후에는, 스택이 빌 때까지 계속 스택의 top을 빼고 해당 좌표의 상하좌우를 살표 보며 스택에 넣어주면 된다.
BFS랑 비슷해서 자세한 건 생략하되, BFS랑 차이점인 DFS만의 진행 양식(깊이 탐색)을 보자.

BFS라면, 이 상태에서 (0(행),2(열))을 탐색하겠지만, DFS는,

이렇게 아래로 내려간다. 이게 깊이(DFS)와 너비(BFS)의 가장 큰 차이점이다.
(그래도 최종적인 방문 결과는 똑같다)
구현
#include <bits/stdc++.h>
using namespace std;
#define X first
#define Y second // pair에서 first, second를 줄여서 쓰기 위해서 사용
int board[502][502] =
{{1,1,1,0,1,0,0,0,0,0},
{1,0,0,0,1,0,0,0,0,0},
{1,1,1,0,1,0,0,0,0,0},
{1,1,0,0,1,0,0,0,0,0},
{0,1,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0} }; // 1이 파란 칸, 0이 빨간 칸에 대응
bool vis[502][502]; // 해당 칸을 방문했는지 여부를 저장
int n = 7, m = 10; // n = 행의 수, m = 열의 수
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1}; // 상하좌우 네 방향을 의미
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
stack<pair<int,int> > S;
vis[0][0] = 1; // (0, 0)을 방문했다고 명시
S.push({0,0}); // 스택에 시작점인 (0, 0)을 삽입.
while(!S.empty()){
pair<int,int> cur = S.top(); S.pop();
cout << '(' << cur.X << ", " << cur.Y << ") -> ";
for(int dir = 0; dir < 4; dir++){ // 상하좌우 칸을 살펴볼 것이다.
int nx = cur.X + dx[dir];
int ny = cur.Y + dy[dir]; // nx, ny에 dir에서 정한 방향의 인접한 칸의 좌표가 들어감
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; // 범위 밖일 경우 넘어감
if(vis[nx][ny] || board[nx][ny] != 1) continue; // 이미 방문한 칸이거나 파란 칸이 아닐 경우
vis[nx][ny] = 1; // (nx, ny)를 방문했다고 명시
S.push({nx,ny});
}
}
}위는 바킹독님의 DFS 기본 코드인데, BFS와 거의 비슷해서 BFS를 공부한 상태라면,
문제없이 이해가 된다.
BFS vs DFS
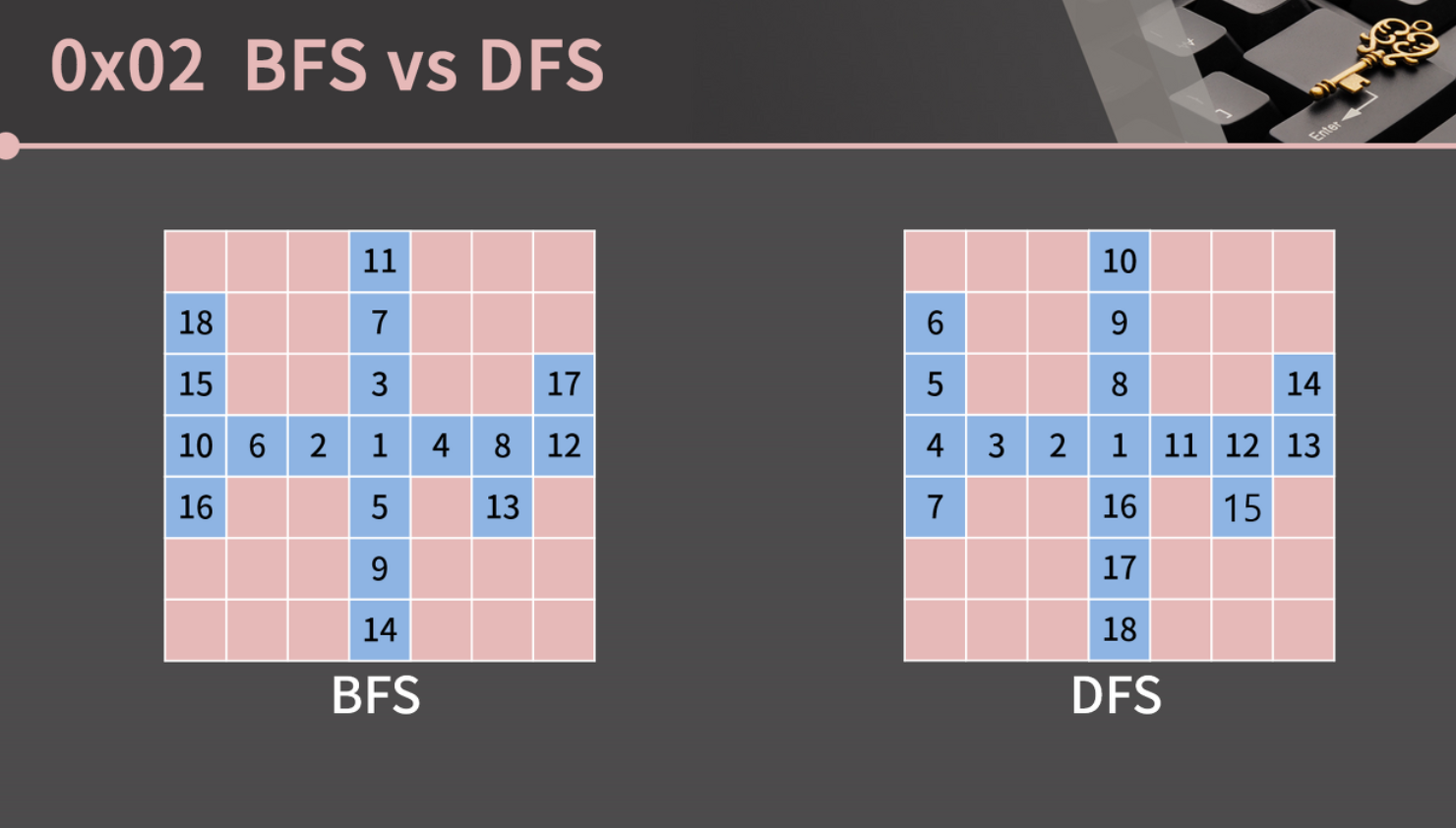
위와 같이, BFS는 큐를 쓰고, DFS는 스택을 쓴다는 차이가 있지만,
주변을 탐색할 원소를 (큐/스택)에서 빼내고 살펴본다는 알고리즘의 흐름은 같다.
쉽게 말해 그림상으로 봤을 때 BFS는 반지름이 점점 커지는 원을 그리며 닿는 칸들을 방문하는 반면,
DFS는 한 방향으로 쭉 나간 다음, 다음 방향으로 쭉 나간다.
+📌BFS에선 가능한 거리계산은 DFS로는 힘들다. 그래서 다차원배열에서 순회하는 문제를 풀 땐, BFS를 사용하도록 하자.
+ 뒤에 그래프/트리 자료구조를 공부할 때 DFS가 필요하니 DFS도 공부해야 한다.
'Problem Solving > Algorithm' 카테고리의 다른 글
| [Algorithm] 재귀 (0) | 2023.08.30 |
|---|---|
| [Algorithm] BFS (0) | 2023.08.26 |
| [Algorithm] 연결리스트 (0) | 2023.08.26 |
| [PS] 코드 작성 시 참고사항 (0) | 2023.08.26 |
| [PS] 시간, 공간복잡도 (0) | 2023.08.26 |
