
바킹독님의 강의를 참고하였습니다.
https://blog.encrypted.gg/category/강좌/실전%20알고리즘
'강좌/실전 알고리즘' 카테고리의 글 목록
blog.encrypted.gg
+ 해당 카테고리엔 알고리즘 문제풀이와 관련된 내용을 업로드.
+ 기록해두고 싶은 부분만 정리해 둠.
알고리즘 설명

"너비"를 우선으로 방문한다.
원래 BFS는 그래프라는 자료구조에서 모든 노드를 방문하기 위한 알고리즘이다.
여기서 말하는 그래프는 오른쪽 그림과 같은 모양의 그래프이고, 정점과 간선으로 이루어진 자료구조이다.
(내 생각) 설명 백날 듣는 것 < 예시 보고 짜보는 것
이라고 생각하기에 코드를 보자..
STL pair
#include <bits/stdc++.h>
using namespace std;
int main(void) {
pair<int, int> p;
p= {1,2}; // pair에 값 넣기
queue< pair<int, int> > q; // 이렇게 응용 가능(특히 좌표 갖고 놀 때)
}들어가기 앞서, 좌표를 갖고 놀 일이 많아서 STL의 pair를 사용하면 두 자료형을 묶어서 갖고 놀 수 있기 때문에
더 쉽게 해결할 수 있다.
예시

우리의 목표는 (0,0)과 상화좌우로 이어진 모든 파란색 칸을 확인하는 것이다. [(행, 열)로 표기할 거임]

BFS 알고리즘에서는 좌표를 담을 큐가 필요하다.
일단 (0,0)에 있으므로, 방문했다는 표시를 남기고, 해당 칸을 큐에 넣는다.
이 초기세팅을 끝낸 후에는, 큐가 빌 때까지 계속 큐의 front를 pop 하고
해당 좌표의 상하좌우를 살펴보면서 큐에 넣어주는 작업을 반복한다.
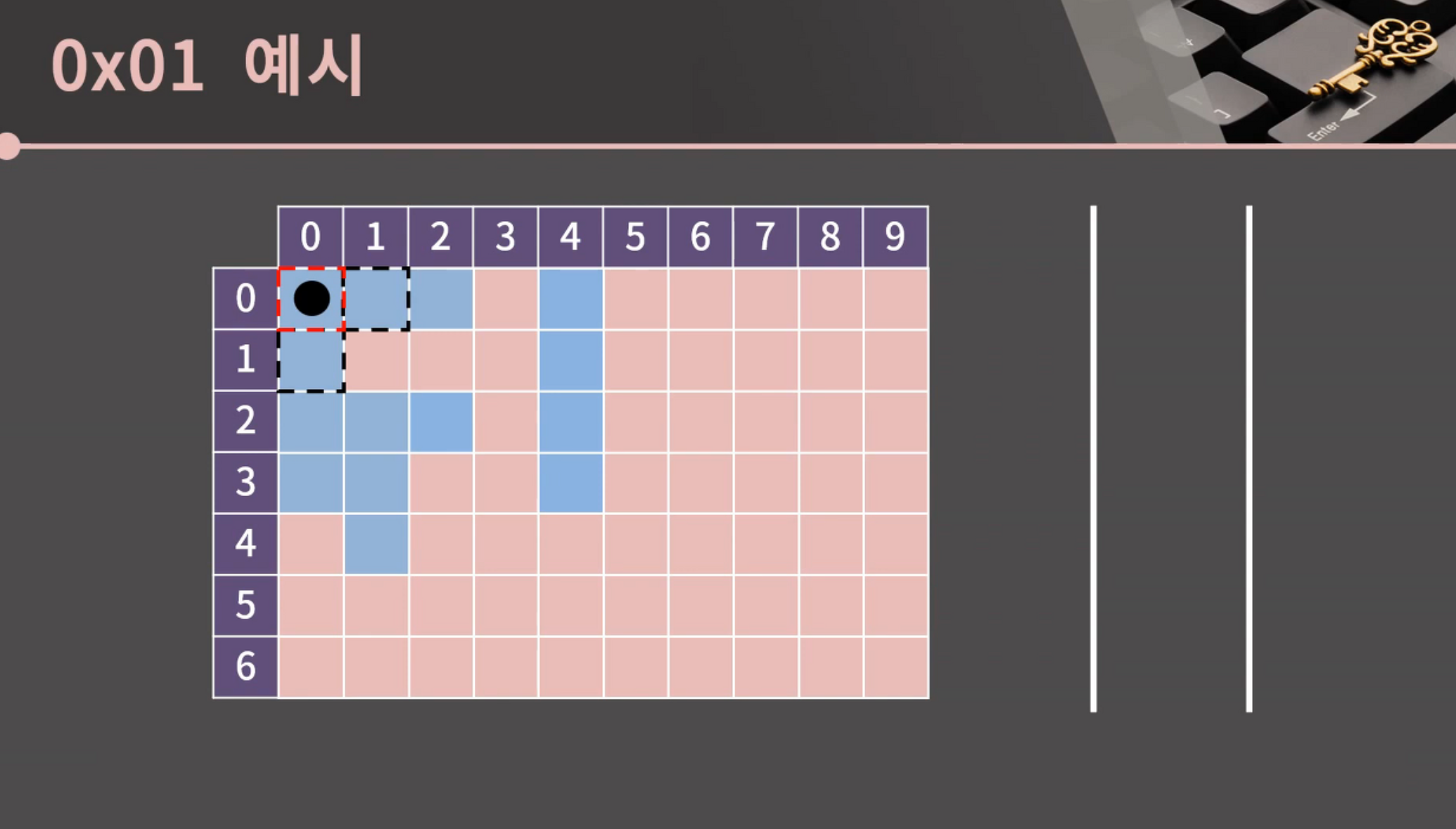
이 상황에서 큐의 front는 (0,0)이니까 pop을 해줌.
그리고 상하좌우 칸 중 파란 칸+아직 방문 안 한 칸을 찾을 거임.

위와 동일하게, 파란 칸+아직 방문 안 한 칸이 상/하에 있으므로 체크표시를 하고 큐에 넣는다.
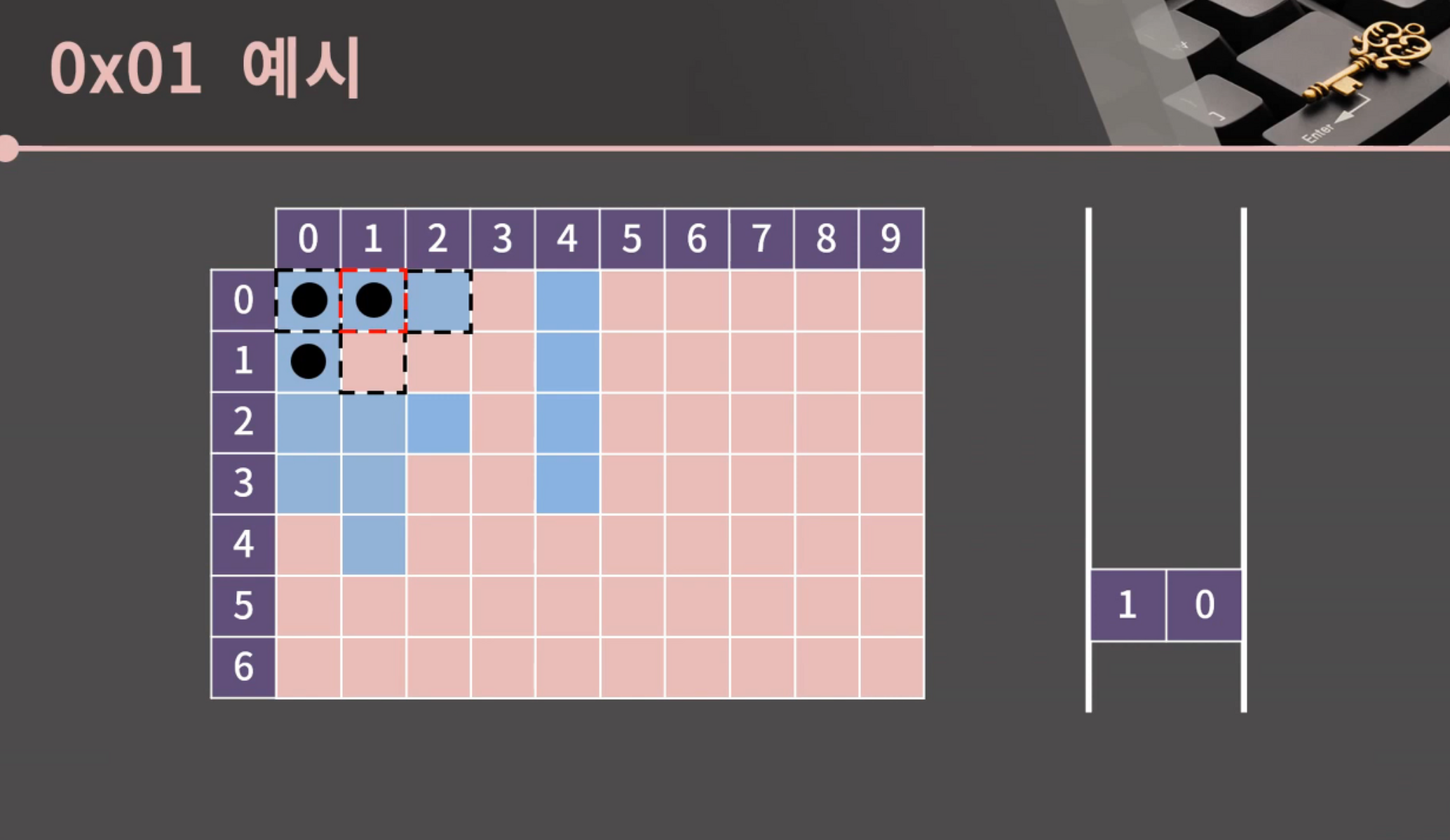
front가 (0,1)이었으므로 pop 해주고, (0,1)의 상하좌우를 확인한다.
(1,1)은 빨간 칸이고, 유일하게 (0,2)만 "방문 안 한 파란 칸"이다.

그래서, (0,2)를 큐에 넣는다.

그리고 이젠 (1,0)을 pop(큐에서 꺼내서) 그 칸에 상하좌우로 인접한 칸에 대해 3번을 진행한다.
이후론, 동일한데, 큐가 한번 초기화될 때까지만 보겠다. (궁금하면 킹독이햄 블로그 ㄱㄱ)




이렇게 계속 반복하다 보면,

이렇게, 한 이어져 있는 영역을 다 탐색했다면 큐가 비워지게 된다.

이번 예시의 과정인데, 맨 위의 예시들을 집중해서 정독한 후, 이 설명을 보면 좋다.
(나는 처음에 언제 pop을 하는지 헷갈렸었는데, 그냥 이 녀석(X)의 상하좌우를 탐색해야지~ 할 때 X를 pop 하면 된다.)
과정을 잘 설명해 두셔서 이 내용 그대로이다.
구현
#include <bits/stdc++.h>
using namespace std;
#define X first
#define Y second // pair에서 first, second를 줄여서 쓰기 위해서 사용
int board[502][502] =
{{1,1,1,0,1,0,0,0,0,0},
{1,0,0,0,1,0,0,0,0,0},
{1,1,1,0,1,0,0,0,0,0},
{1,1,0,0,1,0,0,0,0,0},
{0,1,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,0} }; // 1이 파란 칸, 0이 빨간 칸에 대응
bool vis[502][502]; // 해당 칸을 방문했는지 여부를 저장
int n = 7, m = 10; // n = 행의 수, m = 열의 수
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1}; // 상하좌우 네 방향을 의미
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
queue<pair<int,int> > Q;
vis[0][0] = 1; // (0, 0)을 방문했다고 명시
Q.push({0,0}); // 큐에 시작점인 (0, 0)을 삽입.
while(!Q.empty()){
pair<int,int> cur = Q.front(); Q.pop();
cout << '(' << cur.X << ", " << cur.Y << ") -> ";
for(int dir = 0; dir < 4; dir++){ // 상하좌우 칸을 살펴볼 것이다.
int nx = cur.X + dx[dir];
int ny = cur.Y + dy[dir]; // nx, ny에 dir에서 정한 방향의 인접한 칸의 좌표가 들어감
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; // 범위 밖일 경우 넘어감
if(vis[nx][ny] || board[nx][ny] != 1) continue; // 이미 방문한 칸이거나 파란 칸이 아닐 경우
vis[nx][ny] = 1; // (nx, ny)를 방문했다고 명시
Q.push({nx,ny});
}
}
}위는 바킹독님의 구현예시인데, 참고하고 본인 편한 대로 변형해서 사용하면 좋다.(직접 처음부터 짜보는 게 중요하다고 생각)
코드를 내 나름대로 해독해 보면,
- board [][]에 맵을 담음 (0은 갈 수 없는 칸, 1은 밟을 수 있는 칸)+실제 문제에선 이중 for문으로 입력받아야 함 보통.
- vis [][]는 이미 밟은 땅인지 확인하는 boolean 타입의 배열.
- n, m 은 문제에서 주어지는 맵의 행/열 크기.
- dx, dy는 상하좌우를 탐색할 때 필요한 방향벡터라고 생각하면 됨.
- queue <pair <int, int>>Q로 pair <int, int>(좌표)를 집어넣을 큐를 Q라는 변수에 담음.
- vis [0][0]=1 은 (0,0)에서 시작하니까 이미 밟은 땅이란 걸 표기해 주기 위함.
- Q.push({0,0}) 도 마찬가지로, 큐에 넣어주는 작업.
- while(! Q.empty()) => 큐가 다 텅텅 빌 때까지 반복함.
- cur에 큐(Q)의 front()를 담고, pop 해줌
- for문은 상하좌우탐색의 시작이고, 방향이 4개니까 4번 반복하는 것.
- 이때 dx , dy를 사용해서 nx, ny(다음 밟을 좌표)가 범위 밖인지, 이미 방문한 땅은 아닌지 체크함.
- 모든 예외경우를 통과하고 새로운 땅을 밟으면, vis에 (nx, ny)를 방문했다고 표시해 주고,
- (nx, ny)를 큐(Q)에 넣어준다(push)

위는 직접 짜보며 겪을 수 있는 문제사항들이다.
- 1번은 자명하고
- 2번은 큐에 넣을 때 체크하지 않고 큐에서 뺄 때 체크하는 경우인데, 이렇게 되면 같은 칸이 큐에 여러 번 들어가 시간초과/메모리 초과가 발생할 수 있다.
- 3번은 nx, ny의 제한을 잘해두어야 한다는 뜻.
영역의 개수&넓이


이 문제의 1,2 번은 각각 상하좌우로 연결된 그림의 크기 알아내기 / 도화지에 있는 모든 그림 찾아내기이다.
전자는, 큐에서 pop을 몇 번 하는지만 세면 끝이지만, 후자는, 고민이 필요하다.
사실 난 바킹독님의 글을 처음 봤을 땐 후자가 이해되지 않아서 직접 문제를 풀어보았는데,
그냥 간단하게 이중 for문으로(각 좌표를 하나씩 탐색) 새로운 땅을 언제 새로 탐색하는지만 카운트해 주면 그림의 개수를 얻을 수 있다.
+ 그림의 크기는 pop 한 번당 그림 크기를 저장할 변수에 +1 해주고, max로 비교해 주면 가장 큰 그림을 구할 수 있다.
(내가 보려고 쓰는 글이니 코드가 궁금하다면 킹독이 햄 블로그 ㄱㄱ)
최단경로


위 문제는 맵을 입력받고 원점부터 도착지까지의 최단거리를 구하는 문제이다.

최단거리를 구할 땐 그냥 이거 하나만 기억하면 된다.
체크를 하긴 하는데, 멀어진 거리만큼 체크를 한다.
=> 이러면 위의 사진과 같이 최단거리가 마지막 땅의 체크표시수가 된다. (그냥 그림 보는 게 이해가 편함)
시작점이 여러 개일 때


이미 익은 토마토가 1개였다면 하던 BFS와 비슷한데, 이게 여러 개일 수 있으니 고민을 해야 한다.
각 익은 토마토들에 대해 해당 위치를 시작점으로 하는 BFS를 한 번씩 다 돌리는 방법을 떠올릴 수 있지만, 그럼 시간복잡도가 O(N^2M^2)
이 되어버려 시간 내로 해결이 안 된다.
=> 그냥 모든 시작점을 큐에 넣고 그냥 BFS 돌려버리면 됨.
(그냥 문제 풀면서 고통받으면 이해됩니다.)
- 큐에 (처음 익어있던 토마토) 0이 두 개 들어감.
- 왼쪽 토마토(0,0)부터, 아래하나 익음(1)
- 오른쪽 토마토도 바로 진행, 좌/상/우 세 개 익음(1)
위 과정을 언제 pop 하고 push 하는지 생각하면서 이해하면 편하다.

3차원 토마토 농장도 있습니다 ㅋㅋ
ㄱㄱ
=>3차원이면 STL의 tuple을 이용할 것
시작점이 두 종류일 때
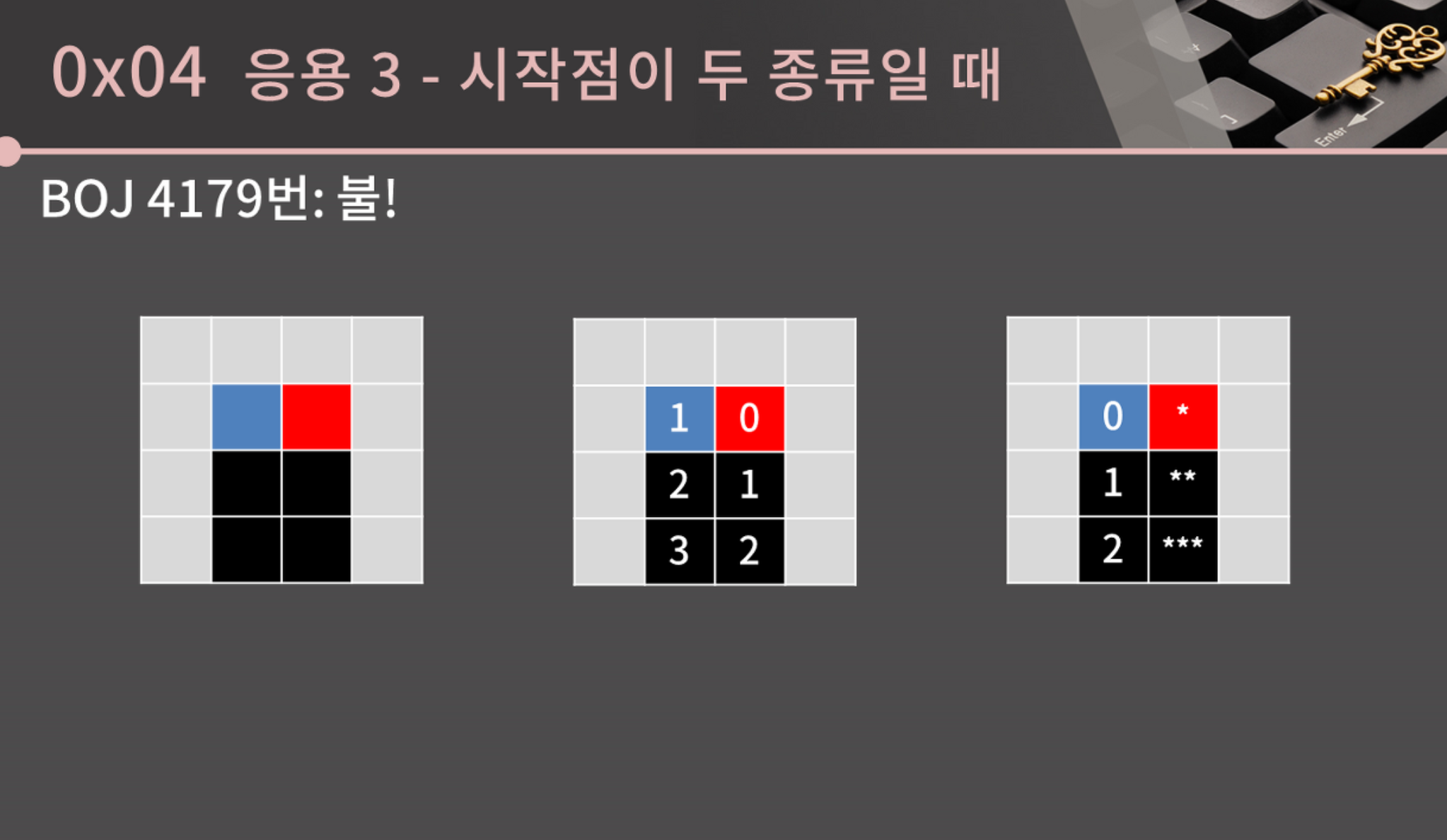

지훈이의 탈출도 처리를 해주어야 하고, 불의 전파도 처리를 해주어야 한다.
- 지훈이는 내버려 두고, 불에 대한 BFS를 돌려서 각 칸에 불이 전파되는 시간을 다 적어둠
- 사진상 두 번째 그림이 불이 각 칸의 불 전파시간을 의미함
- 이제 지훈이를 BFS돌림
- 이때 지훈이가 특정 칸을 x시간에 최초로 방문할 수 있는데 그 칸에는 x시간 or 그 이전에 불이 붙어버리면 그 칸을 못 감
- 그림에선, **칸에 지훈이는 2시간이 될 때 방문하는데, 저 칸은 이미 1시간 전에 전파되어서 못 감
흐름은 이렇고 풀어보면 알 수 있다.
이 경우는 위의 토마토 농장과 달리, 두 시작점의 진행상황이 달라서 헷갈릴 수도 있다.
1차원에서의 BFS

이 문제는 지금까지의 문제들이랑은 다르게 2차원 배열 형태가 아니다.
그래서 헷갈리지만, 수빈이가 X에 있다고 할 때 X-1, X+1, 2X로 이동하는 것을 BFS로 어떻게 처리할까 생각해 보며 풀어보자.

수빈이가 위처럼 5에 있었다고 치면, 5에서 BFS를 시작하고,
5에서 갈 수 있는 4,6,10은 거리가 1이 되는 것이다.

이제 이런 식으로 진행이 되어, 4의 왼쪽인 3, 2배인 8에 2가 칠해지게 된다.
이렇게 계속 돌며 동생이 있는 위치의 값이 써지면 답을 찾을 수 있다.
+ BFS의 범위를 설정할 때, 0~100,000으로 하면 되는 거 아닌가 하고 쉽게 생각을(나도 했는데) 할 수 있는데,
문제를 보면 수빈이와 동생의 위치가 0~100,000이라고 했지 수빈이가 이동 중에 반드시 0~100,000 사이에 있어야 한다는 조건은 없다.
=> 이 문제에선 괜찮지만 다른 문제에서는 0~100,000 사이에서만 움직인다는 보장은 없다는 걸 주의하자.
많은 케이스가 존재하는 만큼 중요한 알고리즘이니 확실히 공부해 두는 게 좋을 것 같다.
'Problem Solving > Algorithm' 카테고리의 다른 글
| [Algorithm] 재귀 (0) | 2023.08.30 |
|---|---|
| [Algorithm] DFS (0) | 2023.08.27 |
| [Algorithm] 연결리스트 (0) | 2023.08.26 |
| [PS] 코드 작성 시 참고사항 (0) | 2023.08.26 |
| [PS] 시간, 공간복잡도 (0) | 2023.08.26 |
